Cousera机器学习基石第五周笔记-Machine-Learning-Foundation-Week-5-Note-in-Cousera
Traning versus Testing
Actually,I didn’t fully understand this part of course.However I don’t focus on the theory but application.
I will update this note if possible.
Recap and Preview
Recap: The ‘Statistical’ Learning Flow
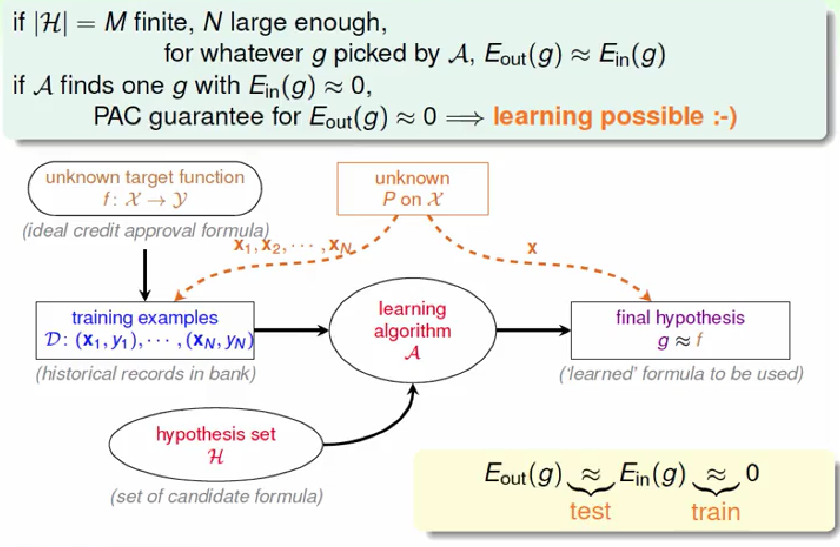
Two Central Questions
1. can we make sure that is close enough to ?
2. can we make small enough?
What role does play for the two questions?
## Trade-off on *M
| small M | large M |
|---|---|
| 1. Yes | 1. No! |
| 2. ,two few choices | 2. Yes!many choices |
using the right M is important
Preview
- Know:
- To do
- establish a finite quantity that replaces M
- justify the feasibility of learning for infinite M
- study to understand its trade-off for ‘right’,just like M
Effective Number of Lines
Where Did M Come From
The BAD event :uniform bound fail M
Where Did Uniform Bound Fail
overlapping for similar hypotheses
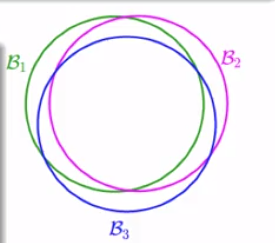
union bound over-estimating
To acoount for overlap,can we group similar hypotheses by kind?
How Many Lines Are There?
In 2D,we can get smaller than lines
Effective Number of Lines
maximun kind of lines with respect to N inputs ,,…,
==effctive number of lines==
In 2D,the effective number of lines
must be
finite ‘grouping’ of infinitely-many lines
wish:
If
effective(N) can replace M and
effective(N)
==learning possible with infinitie lines==