Binary Search
Binary search, examples, templates, notes https://www.youtube.com/watch?v=v57lNF2mb_s
Binary Search
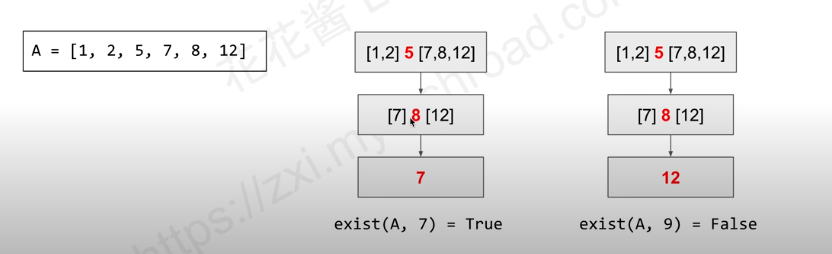
The original form of this problem is: given an array, find whether a number exists in the array and return its position.
A key characteristic: the input is sorted and has no duplicates.
Binary search actually divides the array into three parts. First check if the number is the middle one. If not, search the left or right half based on size comparison. Each time the entire array is halved.
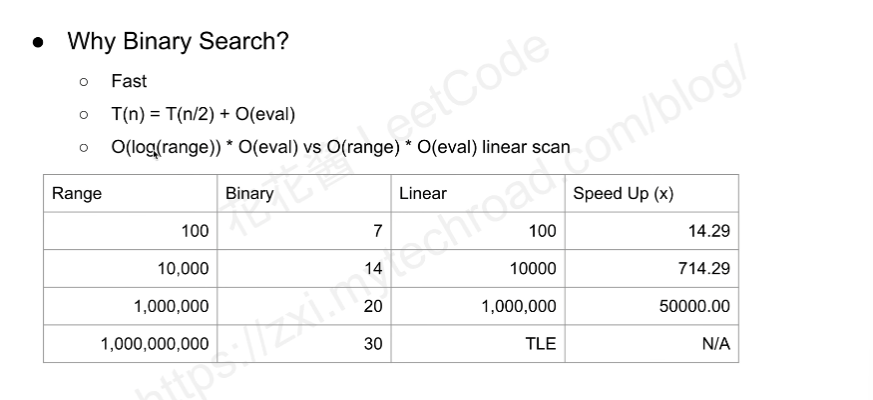
A very obvious feature of binary search is that it’s fast.
A template:
#[l,r)
def binary_search(l,r);
while l<r:
m=l+(r-1)//2 # get the middle number
if f(m):return m # optional: check if this number is my solution
if g(m): # determine if the solution range is on the left or right
r=m # new range[1,m) left side
else:
l=m+1 #[m+1,r)
return l # or not foundFor example, a C++ version:
class Solution
{
public:
int search(vector<int> &nums, int target)
{
int left = 0;
int right = nums.size(); // define target in left-closed right-open interval: [left, right)
while (left < right)
{ // because when left == right, [left, right) is an invalid empty space, so use <
int middle = left + ((right - left) >> 1);
if (nums[middle] == target)
{
return middle;
}
if (nums[middle] > target)
{
right = middle; // target in left interval, in [left, middle)
}
else if (nums[middle] < target)
{
left = middle + 1; // target in right interval, in [middle + 1, right)
}
}
// target not found
return -1;
}
};If array values are not unique, you can use two functions from STL:
lower_bound finds the first element greater than or equal to x in the array
upper_bound finds the first element greater than x in the array
lower_bound(first,last,val) [first,last)
If not found, returns the position where the element would be if it existed.
Variant Problems
LeetCode 69
#include<math.h>
using namespace std;
class Solution {
public:
int mySqrt(int x) {
int right=sqrt(x);
int left = 0; // define target in left-closed right-open interval: [left, right)
while (left < right)
{ // because when left == right, [left, right) is an invalid empty space, so use <
int middle = left + ((right - left) >> 1);
if (middle< right)
{
left = middle + 1; // target in right interval, in [middle + 1, right)
}
}
return left;
}
};Yay! I solved it myself!
LeetCode 278
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
int left = 1;
int right = n; // define target in left-closed right-open interval: [left, right)
int middle=0;
while (left < right)
{ // because when left == right, [left, right) is an invalid empty space, so use <
middle = left + ((right - left) >> 1);
if (isBadVersion(middle) ){
right = middle;
// target in left interval, in [left, middle)
}
else
{
left = middle+1 ; // target in right interval, in [middle + 1, right)
}
}
/*Because it's left-open right-closed, need to check if the last one is bad
At this point, we've narrowed down to left>=right
For example, if there are 5 total and the 4th is bad, then left is 4, right is also 4, 4 is false.
If the first one is bad, then left is greater than right
*/
if(isBadVersion(right))
{
return right;
}
else
{return middle;}
}
};Yay! Another one I solved myself!
LeetCode 875 - My first time attempting a medium problem on my own.
As expected, I couldn’t solve it.
This problem requires converting banana eating speed to H (hours).
Given K, how much time is needed to finish eating?
class Solution {
public:
int minEatingSpeed(vector<int>& piles, int H) {
int low = 1, high = 1000000000, k = 0;
while (low <= high) {
k = (low + high) / 2;
int h = 0;
for (int i = 0; i < piles.size(); i ++)
h += ceil(1.0 * piles[i] / k);
if (h > H)
low = k + 1;
else
high = k - 1;
}
return low;
}
};One thing to note is ceil(1.0 * piles[i] / k) - this is the time needed to eat the i-th pile. After finishing, no more eating, so ceil is used.
Another variant - 378
Another medium problem.
No idea how to approach it.
Oh, I see - check how many numbers are smaller than my current number.
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
int n = matrix.size();
int left = matrix[0][0];
int right = matrix[n - 1][n - 1];
while(left < right) {
int mid = left + (right - left) / 2;
int res = 0;
for(int i = 0; i < n; i++) {
res += upper_bound(matrix[i].begin(), matrix[i].end(), mid) - matrix[i].begin();
}
if(res < k) {
left = mid + 1;
}else {
right = mid;
}
}
return left;
}
};The idea is to use upper_bound to count how many numbers are smaller than the middle value.
For each row, I do an upper_bound with parameters: first value of this row, last value of this row, and the middle value of the entire matrix.
upper_bound returns the index of the first element greater than the matrix’s middle value.
If this index is smaller than k, it means the matrix middle value is not large enough, i.e., the answer is on the right side.
Since this ends when they’re equal, just return left directly.
Summary: The most important thing for this type of problem is finding g(m). The rest is just applying the template.